9.1 Failure Theories
        Types of Failure | Max. Normal Stresses
        Max. Shear Stress | Max. Distortional Energy

» Types of Failure
In general there are two basic methods in which materials FAIL:

    •Brittle Failure or Fracture occurs when a material breaks in two after only a small amount, if any, plastic deformation. Ceramics such as chalk and concrete are examples of materials which exhibit brittle failure.
    •Ductile Failure or Yielding occurs when a material exceeds a its elastic range and undergoes permanent (plastic) deformation. Metals such as aluminum, steel and copper are examples of materials which exhibit ductile failure.

» Maximum Normal Stress
The MAXIMUM NORMAL STRESS FAILURE THEORY states that when the Maximum Normal Stress in any direction of a Brittle material reaches the Strength of the material - the material fails. Thus, finding the Principal Stresses at critical locations is important. Mathematically failure occurs when:

sI > SU or sII > SU   (Tension)
|sI| > |SC| or |sII| > |SC|   (Compression)
  • SU is the ultimate strength in Tension
  • SC is the ultimate strength in Compression
  • In general SC > SU for Brittle materials
Max. Normal Stress Failure Surface

» Tresca - Maximum Shear Stress (Plane Stress Only)
The TRESCA YIELD CONDITION states that for ductile materials, when the Maximum Shear Stress exceeds the Shear Strength, tY, the material yields. Recall that for a given plane the The Maximum In- Plane Shear Stress is the average of the In-Plane Principal Stresses.

tmax =
sI sII

2

The two Maximum Out-of-Plane Shear Stresses are:

tmax = max
sI

2
,
sII

2
  • tmax is the Maximum Shear Stress
  • sI is the Maximum Principal Stress
  • sII is the Minimum Principal Stress
  • Note that the Out-of-Plane Principal Stress (sIII) for the strain plane condition is zero

Failure occurs when the maximum of the Three Maximum Shear Stresses reaches the shear yield stress, tY.

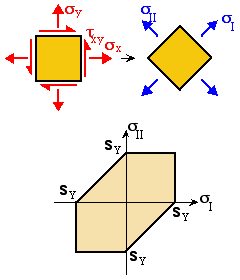
The above plot is a Failure Map. If the In-plane Principal Stresses lie outside the shaded zone, failure occurs.

  • Under a uniaxial load, sII = sIII = 0. Thus, the axial yield stress is sI = SY = 2tY. The Maximum Shear Stress Theory predicts that the Shear Yield Stress is half the Axial Yield Stress.
  • When the In-Plane Principal Stresses are the same sign (1st and 3rd quadrant), the Maximum Shear Stress in the system is Out-of-Plane.
    When the In-Plane Principal Stresses are opposite sign (2nd and 4th quadrant), the Maximum Shear Stress in the system is In-Plane.

» von Mises - Maximum Distortional Energy
The von MISES YIELD CRITERIA states that a material will fail when the von Mises Equivalent Stress (so exceeds the Axial Yield Stress (SY). The von Mises Equivalent Stress is defined by:

2so2 = (sI - sII)2 + (sII - sIII)2 + (sIII - sI)2

When so = SY the material is deemed to have yielded.

For Plane Stress the von Mises Failure Criterion reduces to:

so =
sI2 sIsII + sII2
1/2
SY
or
so =
sx2 sxsy + sy2 + 3ty2
1/2
SY

Using the above relationship, the von-Mises relationship predicts that ratio of the Axial Yield Stress to the Shear Yield Stress is: SY = 1.732 tY.

From the Tresca condition: SY = 2 tY.

In general, metals tend follow the Axial Yield Stress-Shear Yield Stress relationship of von Mises, making von Mises more accurate. However, von Mises is harder to use.

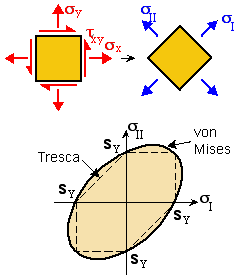
von Mises Failure Surface

The above plot is a Failure Map. If the In-plane Principal Stresses lie outside the shaded zone, failure occurs.