Ex. 9.1.1 | Ex. 9.1.2



| 9.1 Failure Examples Ex. 9.1.1 | Ex. 9.1.2 |



|
|
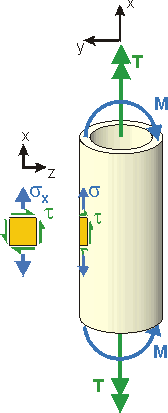
Example 9.1.1 - Femur Failure Background: The shaft of a femur (thigh bone) can be approximated as a hollow cylinder. The significant loads that it carries are torques and bending moments. Given: The femur shaft has an outside diameter of 24 mm and an inside diameter of 16 mm. The tensile strength of bone is taken to be Su = 120 MPa. Req'd: The effective moment the bone can take without failure. Consider only torsion and bending loads, and take the bone to be a brittle material. |
 Image: eSkeletons Project |
|
Solution: Since the bone is brittle, it follows the Maximum Normal Stress criteria. If the maximum Principal Stress is greater than the material Tensile Strength, sI > Su, the bone fails (fractures). The element is taken on the left side of the femur as we look at it; the element is in the z-x plane. The Maximum Principal Stress is: 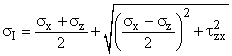 The contributing stresses are: 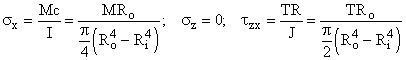 Solving the geometric terms: so: t = TRo/J = 45.9 MPa Reducing the sI equation: 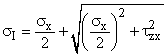 |
| |
|
and rearranging: 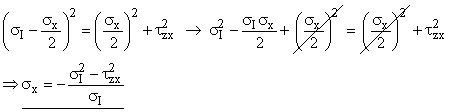 For the bone to break, sI = Su = 120 MPa. Using the Bending Stress formula (s=Mc/I), the Moment to break the bone is:
| ||
|
Solution: Step 1: The Tresca Condition is based on the Maximum Shear Stress. The Max. In-Plane Shear Stress is given by:
To find the Out-of-Plane Shear Stresses, we need to find the In-Plane Principal Stresses:
Considering all directions, for Plane Stress, the Maximum Shear Stress, tmax is:
Thus:
| ||||||||
|
Step 2: The von Mises Criterion is based on Maximum Distortion Energy. The von Mises (or Equivalent) Stress for a Plane-Stress element is:
If the Equivalent Stress, so, exceeds the uniaxial Yield Stress, the material is deemed to have yielded. Using either equation, solving for the equivalent stress gives : so = 12.2 ksi
COMMENTARY
| ||||||

|


|