|
» Discretely and Continually Varying Shafts
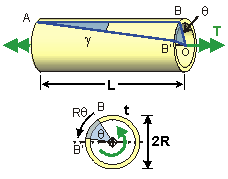
To solve problems involving DISCRETELY VARYING SHAFTS, break up the Shaft into lengths over which all the values of Force, Area and Modulus are constant. The total angle of rotation can then be obtained by treating each section of bar as a Uniform Torsion Member:
Similarly, for problems involving CONTINUALLY VARYING SHAFTS, the Angle of Twist can be determined by integrating over the length of the member:
| qtotal = |

L |
dq = |

L |
T(x) dx

J(x) G(x) |
|
|
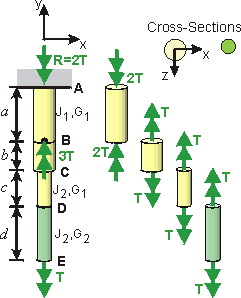
Discretely Varying Torsion Member.
|