Uniform Bar | Discretely Varying Bar
Continually Varying Bar | Displacement Method


|
4.1 Axial Members
Uniform Bar | Discretely Varying Bar Continually Varying Bar | Displacement Method |


|
|
» Discretely Varying Axial Member
|
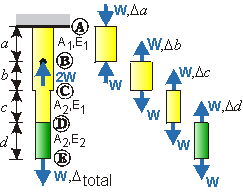
Discretely Varying Axial Member. |
|
» Continually Varying Axial Member
To solve problems involving Continually Varying Loads, Areas, or Modulus, the deflection can be determined by integrating over the length of the member:
|
|
» Displacement Method
Also note that the Stiffness of an Axial Member is given by:
|

|



|