4.1 Axial Member Examples
        Ex. 4.1.1 | Ex. 4.1.2 | Ex. 4.1.3

Example 4.1.1

Given: A stepped-bar (areas A1, A2) made of two materials (moduli E1, E2), acted on by forces 2W (upward at Pt. B) and W (downward at Pt. E).

Req'd: Total elongation of the bar, Dtotal.

Sol'n:

Step 1. Equilibrium - Solve for forces:
Since loads are only vertical forces acting along the same line of action, the reaction force at the ceiling is R=W (downward at Pt. A). The other forces are shown at right.

Bar broken up into lengths with constant force, area and modulus.

Step 2. Elongation/Force Relation:
To solve for elongations, break up the bar into lengths over which all the values (force, area and modulus) are constant.

The top length of the bar AB, has length a, area A1, modulus E1, and carries force Pa = -W (compression). The change in length of AB is:

Since AB is in compression, it shortens: Da<0. Therefore, Point B "moves up." Taking each of the other lengths with constant force, area and modulus:

All other segments of the bar (BC, CD, DE) are in tension, so each get longer.

Step 3. Compatability:
The total elongation or deflection, Dtotal, is then:

Here, the deflection of any point (upward or downward) depends on the extension (compression) of the bar(s) above it.

Example 4.1.2

Given: A conical pillar supports a weight, W.

Req'd: The shortening of the column due to the load. Neglect the weight of the column. Measure x from the top of the pillar.

Sol'n: Break up the column into lengths where the properties are "constant".

Here, it is differential length dx. Over dx, the force, area and modulus are essentially constant. By finding the elongation, dD, of each dx,

and adding them up - integrating - we find the deflection of the bar.

  • P(x) = -W (compression) and E(x)=E are constant over L.
  • Area A(x) varies from pR2 at the top to p(4R)2 at the bottom. We must find an equation for A(x)=p[R(x)]2, which is done at the right.

Knowing A(x), sum all of the dD over length L:

Bar broken up into lengths with constant force, area and modulus. The stress at any point is s(x) = P(x)/A(x).

    Radius as a function of x:

  • At endpoints:
    • R(x=0) = R;
    • R(L) = 4R.
  • R increases linearly from R to 4R:

R(x) = R[1+3x/L].

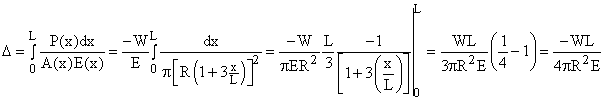
The deflection is "negative" - the column shortens. The Effective Stiffness for the cut-off cone acted on by constant force throughout its length is Keff = |W/D| = (4pR2E)/L

Example 4.1.3

Given: A circular stepped bar, constrained on both ends, is subjected to a force P which causes a deflection of d at point C as shown at right.

Req'd: Use the Displacement Method to determine the force, P, and the stiffness of the bar, K, in terms of the displacement, d, the Young's Modulus, E, and the geometric parameters of the bar.

Sol'n:

Solve this problem using the three steps spelled out for the Displacement Method:

Step 1. Compatibility: Geometric constraint of the system require that

DAC = -DCB = d

Step 2. Hooke's Law: The forces in the two members can be related to the displacements as follows:

F = sA,   s = Ee,   e =
D

L
 , therefore
FAC =
AACEACDAC

LAC
 ,     FCB =
ACBECBDCB

LCB

Step 3. Equilibrium: Equilibrium requires that P + FAC = FCB. Combining gives:

P =
ACBECBDCB

LCB
 -
AABEABDAB

LAB
 =
3AE

L
 d

The Stiffness is then:

K =
P

d
=
3AE

L