Cylindrical Pressure Vessels | Spherical Pressure Vessels
Deformation of Pressure Vessels



| 4.2 Pressure Vessels Cylindrical Pressure Vessels | Spherical Pressure Vessels Deformation of Pressure Vessels |


 |
|
» Spherical Pressure Vessels
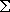 F = 0 F = 0  ppR2
= sS(2pRt)
ppR2
= sS(2pRt)
|
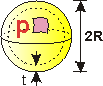
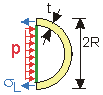 Spherical Stress FBD. |
|
» Deformation of Pressure Vessels
| |||||||||||||||

|


 |