4.4 Energy Methods Examples
        Ex. 4.4.1

Example 4.4.1

Given: Consider the frame ABC at right. The length AB is 10 ft, BC is 20 ft, and angle ABC is 60°. The cross-sectional area of AB is 10 in2 and BC is 2 in2 and Young's modulus is 30x106 psi.

Req'd:
Determine the deflection of the load when P = 20,000 lb


Frame ABC

Sol'n: Form free-body diagram of joint B vertical and horizontal equilibrium give:

FBCsin(60) = P
and
FAB + FBCcos(60) = 0

Solving for the forces:

FBC = 1.15 P     and     FAB = -0.577 P

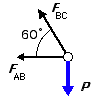
FBD of Joint B

Recall the internal energy of a bar of length L and cross-sectional area A is:

U =
P2L

2AE

Applying this formula to AB and BC, the total energy of the bars is:

U =
FAB2LAB

2AABE
 +
FBC2LBC

2ABCE
U =
P2

2(30x106)
(-0.577)2(120)

10
 +
(1.15)2(240)

2
U = 2.71x10-6 · P2

The work done by the applied force P is:

W =
Pd

2

This work is equal to the internal energy. Therefore:

Pd

2
= 2.71x10-6 · P2

Solving for d we get:

d = 2(2.71x10-6)P

When P = 20,000 lb we get:

d = 2(2.71x10-6)(20,000)
d = 0.108 in