8.3 Mohr's Circle
        Mohr's Circle Construction | Using Mohr's Circle
        Mohr's Circle for Strain

» Mohr's Circle
MOHR'S CIRCLE is a plane stress transformation tool developed by Otto Mohr in the late 19th century. Mohr realized that when the stress transformation equations were manipulated in a certain way they matched the equation of a circle. When plotted the stress is plotted on the s-t axis system, we get Mohr's Circle:

(sx' save)2 + (tx'y' 0)2 = tmax2

Mohr's Circle
Recall that:
save =
sx + sy

2
  and   tmax =
sx sy

2
2
+
txy
2
1/2

» Mohr's Circle Construction
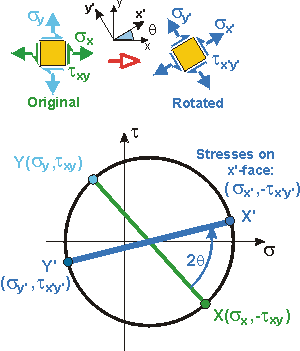
The steps for CONSTRUCTING MOHR'S CIRCLE are given below:
(A module for the dynamic construction of the Mohr's Circle is available by clicking here)

Step 1. Draw an "x-y" axis on graph paper with the horizontal axis labeled s and the vertical axis labeled t or tCW (CW for clockwise).

Step 2. Plot points: X(sx, -txy) and Y(sy, txy), using the correct convention for positive/negative stresses. Plot Shear Stress above the s-axis if it causes a clockwise rotation.

Step 3. Draw a line connecting X(sx, -txy) and Y(sy, txy). This is the diameter of the Mohr's Circle and has a magnitude of twice the maximum shear stress. Where the line intersects the s-axis is the center of the circle, and gives the average normal stress.

Step 4. Draw the circle, with center at (save, 0)
The stresses are
drawn POSITIVE.

KEY POINTS:

  • A Rotation of 2q in MOHR's CIRCLE corresponds to a rotation of q in the STRESS ELEMENT.
  • The points where the circle intersects the s-axis define the Principal Stresses, sI and sII.
  • The radius equals the Maximum Shear Stress, or half the difference of the Principal Stresses:
    R = tmax = (sI - sII)/2
    .
  • If you have plotted the graph to scale, you can use geometric relationships to solve for the values of the Principal Stresses ( save ± R) and Maximum Shear Stresses (R).

» Using Mohr's Circle
The power of Mohr's Circle lies in its simplicity.

To find the stress state at any angle q (sx', sy', tx'y'), simply rotate the X-Y diameter in Mohr's Circle by 2q.

The new endpoints X' Y' correspond to the the new stress state X'(sx', -tx'y') - Y'(sy', tx'y').

» Mohr's Circle for Strain
A MOHR'S CIRCLE for STRAIN can also be used. Here the points that are plotted are X( ex, -gyx/2) and Y(ey, gxy/2). As with the Strain Transformation Equations, use g/2 in place of t.