Ex. 8.1.1 | Ex. 8.1.2



| 8.1 Stress Transformation Examples Ex. 8.1.1 | Ex. 8.1.2 |



|
|
Sol'n: |
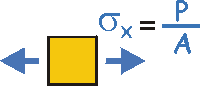 |
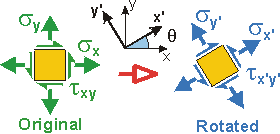
Step 2: The Stress Transformation Equations are:
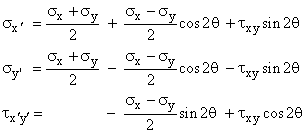 Here, sy and txy are both zero, so the equations simplify to: sx' = 0.5 sx(1+cos2q)
= Stress acting Normal to Weld
Or, the Normal and Shear Stresses acting on the weld are:
|
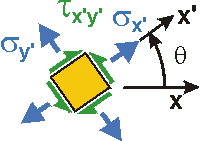
| ||
|
Note: the Principal of Invariance requires that: sx' + sy' = sx + sy = 3.75 MPa + 1.25 MPa = 5.00 MPa | |||
|
Sol'n: 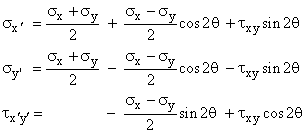
|
 |
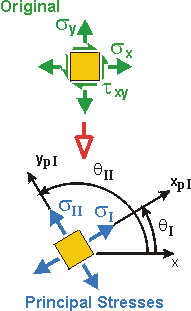
Step 2: Principal Stresses and Angles.
|
| |||||||
Step 3: Maximum Shear Stress
|

| ||||||||

|



|