


| Practice Problem 7-2 |



|
|
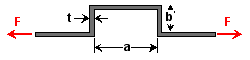
Given: The square aluminum (E = 10 Msi) bar at right is subjected to a tensile force of F = 100 lb. Let t = 1 in., a = 24 in. and b = 5 in. Req'd: Determine the maximum normal stress in the bar. |
|
|
Solution: If the middle section of the bar is isolated and treated as a free-body diagram, it can easily be seen that there is both an axial force and a bending moment acting on the section. The maximum normal stress will thus occur in the middle section of the bar as a result of an axial stress and a bending stress. The axial stress in this section is simply the force divided by the cross-sectional area: sA = F/t2 The maximum bending stress is given by sB = Mc/I, which for a square beam reduces to: sB = 6M/t3 The bending moment is M = F·b. Combining these gives: smax = F/t2 + 6F·b/t3 smax = 100 lb/(1 in)2 + 6(100 lb)(5 in)/(1 in)3 = 3100 psi = 3.1 ksi |

|
 

|