» Deflection
In addition to bending stresses, internal and external loads cause beams to DEFLECT. The shape of the deflected beam is defined by v(x); it is the deflection of the neutral axis with respect to its original condition. The deflected shape is called the ELASTIC CURVE. Deflection and the elastic curve are always:

• Smooth. The slope must be the same at a junction of any two parts of a beam, regardless of the direction from which the common point is approached.
• Continuous. The displacement must be the same at a junction of any two parts of a beam, regardless of the direction from which the common point is approached.

» Governing Equations
Based on the Moment-Shear-Load relations and the beam curvature, the GOVERNING DIFFERENTIAL EQUATION for deflection of an elastic beam is:

v''(x) = d2 v(x) dx2 = M EI

• EI is called the flexural rigidity of a beam.

Expressions for BEAM SLOPE and BEAM DEFLECTION can be gotten by integrating the Governing Differential Equation twice:

v''(x) = M EI Slope =   v'(x) = M EI dx + C1 Deflection =   v(x) = M EI dx + C1 dx + C2

The constants C₁ and C₂ are determined by considering the beam's BOUNDARY CONDITIONS.

» Boundary Conditions
BOUNDARY CONDITIONS are the restrictions imposed on a beams by its supports. In order to solve beam-deflection problems, in addition to the differential beam equations, the boundary conditions must be prescribed at each support. The most common types of boundary conditions are shown at right (click on description below to see example):

• Clamped or fixed support (built-in). The right end of the beam has a clamped support. Therefore the displacement ( v ) and slope ( v' ) must both be zero.
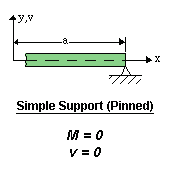
• Simple Support (pin or roller). The right end of the beam has a simple support. Therefore the displacement ( v ) must be zero. The beam is free to rotate (the pin does not resist rotation), therefore the moment ( M ) must also be zero.
• Free End. The right end of the beam is a free end. Therefore the beam is free of moment ( M ) and shear ( V )
• Guided support. The right end of the beam has a guided support and is free to deflect normal to the beam, but is unable to rotate, thus the slope ( v' ) must be zero. Also the support is not capable of resisting shear ( V ).