


| Practice Problem 2-1 |



|
|
Given: A shaft with two gears, A and B, is driven by a motor. Gears A and B are acted upon by tangential forces FA and FB, where FA = 120 lb and FB = 200 lb. The diameters of the gears are: DA = 6 in. and DB =10 in. Req'd: What output torque, TM, is required by the motor to turn the shaft at a constant rate? |
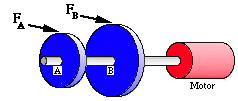
|
|
Solution: For the shaft to turn at a constant rate it must be in equilibrium. This means that the sum of all the torques actingon the shaft must equal zero, therefore: TA + TM - TM = 0 TM = TA + TB TM = (FA)(RA) + (TB)(RB) TM = (120 LB)(3 in) + (200 LB)(5 in) = 1360 in-LB |

|



|